Welcome to fast_bss_eval’s documentation!#
fast_bss_eval is a fast implementation of the bss_eval metrics for the
evaluation of blind source separation. Our implementation of the bss_eval
metrics has the following advantages compared to other existing ones.
very fast
can be even faster by using an iterative solver (add
use_cg_iter=10option to the function call)supports batched computations
differentiable via pytorch
can run on GPU via pytorch
This library implements the bss_eval metrics for the evaluation of blind source separation (BSS) algorithms 1. The implementation details and benchmarks against other publicly available implementations are also available 2.
Quick start#
The package can be installed from pip. At a minimum, it requires to have numpy/scipy installed.
To work with torch tensors, pytorch should also be installed obviously.
pip install fast-bss-eval
Assuming you have multichannel signals for the estimated and reference sources
stored in wav format files named my_estimate_file.wav and
my_reference_file.wav, respectively, you can quickly evaluate the bss_eval
metrics as follows with the function bss_eval_sources() and sdr().
from scipy.io import wavfile
import fast_bss_eval
# open the files, we assume the sampling rate is known
# to be the same
fs, ref = wavfile.read("my_reference_file.wav")
_, est = wavfile.read("my_estimate_file.wav")
# compute all the metrics
sdr, sir, sar, perm = fast_bss_eval.bss_eval_sources(ref.T, est.T)
# compute the SDR only
sdr = fast_bss_eval.sdr(ref.T, est.T)
You can use the sdr_pit_loss() and sdr_loss() to train separation networks with
pytorch and
torchaudio.
The difference with the regular functions is as follows.
reverse order of
estandrefto follow pytorch conventionsign of SDR is changed to act as a loss function
For permutation invariant training (PIT), use sdr_pit_loss(). Use
sdr_loss() if the assignement of estimates to references is known, or
to compute the pairwise metrics.
import torchaudio
# open the files, we assume the sampling rate is known
# to be the same
ref, fs = torchaudio.load("my_reference_file.wav")
est, _ = torchaudio.load("my_estimate_file.wav")
# PIT loss for permutation invariant training
neg_sdr = fast_bss_eval.sdr_pit_loss(est, ref)
# when the assignemnt of estimates to references is known
neg_sdr = fast_bss_eval.sdr_loss(est, ref)
To summarize, there are four functions implemented, bss_eval_sources(),
sdr(), and sdr_pit_loss(), and sdr_loss().
The scale-invariant 3 versions of all these functions are available in functions pre-fixed by si_, i.e.,
Alternatively, the regular functions with keyword argument filter_length=1 can be used.
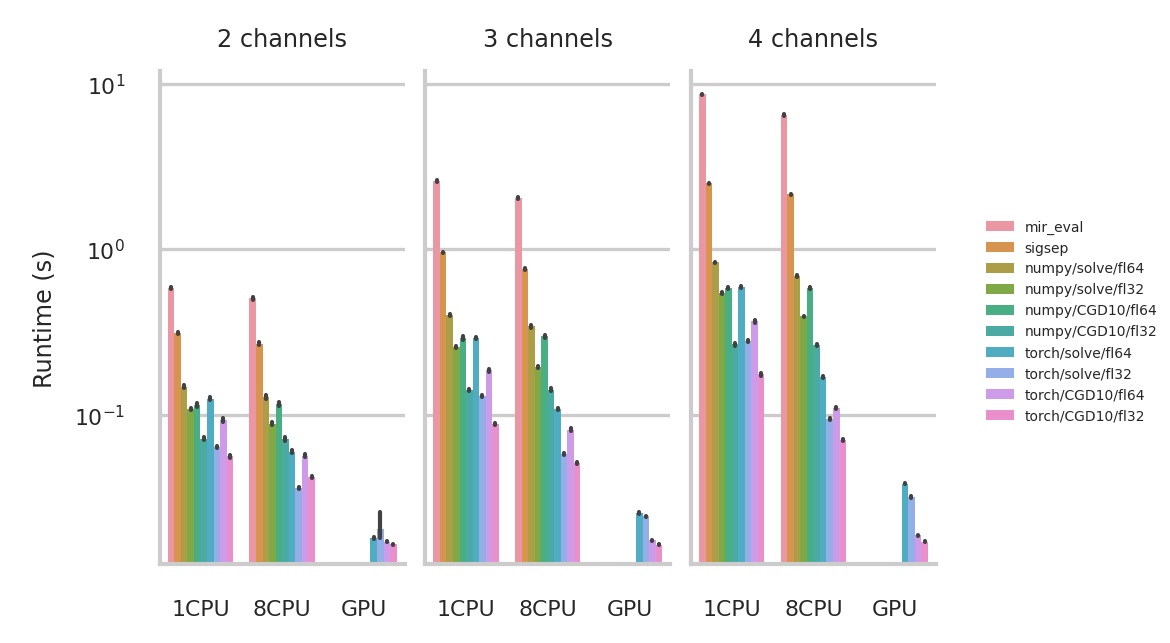
Benchmark#
Average execution time on a dataset of multichannel signals with 2, 3, and 4
channels. We compare fast_bss_eval to mir_eval and sigsep. We further benchmark fast_bss_eval
using numpy/pytorch with double and single precision floating-point
arithmetic (fp64/fp32), and using solve function or an iterative solver (CGD10).
The benchmark was run on a Linux workstation with an Intel Xeon Gold 6230 CPU @
2.10 GHz with 8 cores, an NVIDIA Tesla V100 GPU, and 64 GB of RAM.
We test single-threaded (1CPU) and 8 core performance (8CPU) on the CPU, and on the GPU.
We observe that for numpy there is not so much gain of using multiple cores.
It may be more efficient to run multiple samples in parallel single-threaded
processes to fully exploit multi-core architectures.
bss_eval metrics theory#
\(\newcommand{\vs}{\boldsymbol{s}}\newcommand{\vshat}{\hat{\vs}}\newcommand{\vb}{\boldsymbol{b}}\) We consider the case where we have \(M\) estimated signals \(\vshat_m\). Each contains a convolutional mixture of \(K\) reference signals \(\vs_k\) and an additive noise component \(\vb_m\),
where \(\vshat_m\), \(\vs_k\), and \(\vb_m\) are all real vectors of length \(T\). The length of the impulse responses \(\vh_{mk}\) is assumed to be short compared to \(T\). For simplicity, the convolution operation here includes truncation to size \(T\). In most cases, the number of estimates and references is the same, i.e. \(M=K\). We keep them distinct for generality.
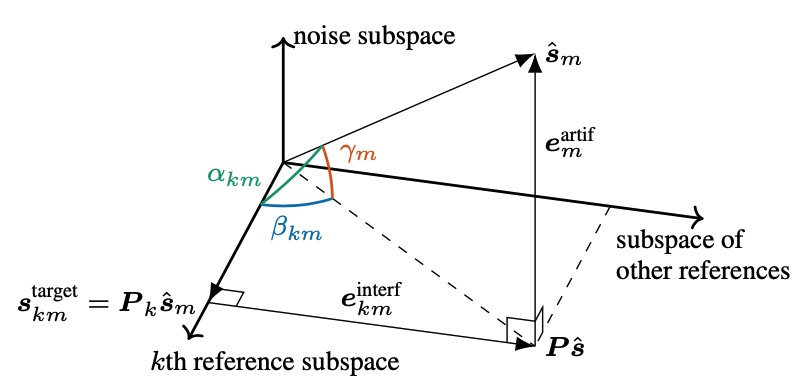
bss_eval decomposes the estimated signal into three orthogonal components corresponding to the target, interference, and noise, as shown in the illustration above.
Rather than projecting directly on the signals themselves, bss_eval allows for a short distortion filter of length \(L\) to be applied. This corresponds to projection onto the subspace spanned by the \(L\) shifts of the signals. Matrices \(\mP_k\) and \(\mP\) are orthogonal projection matrices onto the subspace spaned by the \(L\) shifts of \(\vs_k\) and of all references, respectively. Let \(\mA_k \in \mathbb{R}^{(T + L - 1) \times L}\) contain the \(L\) shifts of \(\vs_k\) in its columns and \(\mA = [\mA_1,\ldots,\mA_K]\), then
Then, SDR, SIR, and SAR, in decibels, are defined as follows,
Finally, assuming for simplicity that \(K=M\), the permutation of the estimated sources \(\pi\,:\,\{1,\ldots,K\} \to \{1,\ldots,K\}\) that maximizes \(\sum_k \text{SIR}_{k\,\pi(k)}\) is chosen. Once we have the matrix of SIR values, we can use the linear_sum_assignement function from scipy to find this optimal permutation efficiently.
The scale-invariant SDR is equivalent to using a distortion filter length of 1 3. The use of longer filters has been shown to be beneficial when training neural networks to assist beamforming algorithms 2 4.
Iterative solver for the disortion filters#
Note
tl;dr If you need more speed, add the keyword argument use_cg_iter=10 to any method call.
As described above, computing the bss_eval metrics requires to solve the systems
for all \(k\) and \(m\). These system matrices are large and solving
directly, e.g., using numpy.linalg.solve, can be expensive. However, these
matrices are also structured (Toeplitz and block-Toeplitz). In this
case, we can apply a much more efficient iterative algorithm based on
preconditioned conjugate gradient descent 5.
The default behavior of fast_bss_eval is to use the direct solver (via the
solve function of numpy or pytorch) to ensure consistency with
the output of other packages.
However, if speed becomes an issue, it is possible to switch to the iterative
solver by adding the option use_cg_iter (USE Conjugate Gradient ITERations) to
any of the methods in fast_bss_eval.
We found that using 10 iterations is a good trade-off between speed and accuracy,
i.e., use_cg_iter=10.
License#
2021 (c) Robin Scheibler, LINE Corporation
The source code for this package is released under MIT License and available on github.
Bibliography#
- 1
E. Vincent, R. Gribonval, and C. Fevotte, Performance measurement in blind audio source separation, IEEE Trans. Audio Speech Lang. Process., vol. 14, no. 4, pp. 1462–1469, Jun. 2006.
- 2(1,2)
R. Scheibler, SDR - Medium Rare with Fast Computations, arXiv:2110.06440, 2021. pdf
- 3(1,2)
J. Le Roux, S. Wisdom, H. Erdogan, and J. R. Hershey, SDR - Half-baked or Well Done?, In Proc. IEEE ICASSP, Brighton, UK, May 2019.
- 4(1,2)
C. Boeddeker et al., Convolutive transfer function invariant SDR training criteria for multi-channel reverberant speech separation, in Proc. IEEE ICASSP, Toronto, CA, Jun. 2021, pp. 8428–8432.
- 5
R. H. Chan and M. K. Ng, Conjugate gradient methods for Toeplitz systems, SIAM Review, vol. 38, no. 3, pp. 427–482, Sep. 1996.
API#
- fast_bss_eval.bss_eval_sources(ref, est, filter_length=512, use_cg_iter=None, zero_mean=False, clamp_db=None, compute_permutation=True, load_diag=None)#
This function computes the SDR, SIR, and SAR for the input reference and estimated signals.
The order of
ref/estfollows the convention of bss_eval (i.e., ref first).- Parameters
ref (
Union[ndarray,Tensor]) – The estimated signals,shape == (..., n_channels_est, n_samples)est (
Union[ndarray,Tensor]) – The groundtruth reference signals,shape == (..., n_channels_ref, n_samples)filter_length (
Optional[int]) – The length of the distortion filter allowed (default:512)use_cg_iter (
Optional[int]) – If provided, an iterative method is used to solve for the distortion filter coefficients instead of direct Gaussian elimination. This can speed up the computation of the metrics in case the filters are long. Using a value of 10 here has been shown to provide good accuracy in most cases and is sufficient when using this loss to train neural separation networks.zero_mean (
Optional[bool]) – When set to True, the mean of all signals is subtracted prior to computation of the metrics (default:False)clamp_db (
Optional[float]) – If provided, the resulting metrics are clamped to be in the range[-clamp_db, clamp_db]compute_permutation (
Optional[bool]) – When this flag is true, the optimal permutation of the estimated signals to maximize the SIR is computed (default:True)load_diag (
Optional[float]) – If provided, this small value is added to the diagonal coefficients of the system metrics when solving for the filter coefficients. This can help stabilize the metric in the case where some of the reference signals may sometimes be zero
- Return type
Union[Tuple[ndarray,...],Tuple[Tensor,...]]- Returns
sdr – The signal-to-distortion-ratio (SDR),
shape == (..., n_channels_est)sir – The signal-to-interference-ratio (SIR),
shape == (..., n_channels_est)sar – The signal-to-interference-ratio (SIR),
shape == (..., n_channels_est)perm – The index of the corresponding reference signal (only when
compute_permutation == True),shape == (..., n_channels_est)
- fast_bss_eval.sdr(ref, est, filter_length=512, use_cg_iter=None, zero_mean=False, clamp_db=None, load_diag=None, return_perm=False, change_sign=False)#
Compute the signal-to-distortion ratio (SDR) only.
This function computes the SDR for all pairs of est/ref signals and finds the permutation maximizing the sum of all SDRs. This is unlike
bss_eval_sources()that uses the SIR.The order of
ref/estfollows the convention of bss_eval (i.e., ref first).- Parameters
ref (
Union[ndarray,Tensor]) – The estimated signals,shape == (..., n_channels_est, n_samples)est (
Union[ndarray,Tensor]) – The groundtruth reference signals,shape == (..., n_channels_ref, n_samples)filter_length (
Optional[int]) – The length of the distortion filter allowed (default:512)use_cg_iter (
Optional[int]) – If provided, an iterative method is used to solve for the distortion filter coefficients instead of direct Gaussian elimination. This can speed up the computation of the metrics in case the filters are long. Using a value of 10 here has been shown to provide good accuracy in most cases and is sufficient when using this loss to train neural separation networks.zero_mean (
Optional[bool]) – When set to True, the mean of all signals is subtracted prior to computation of the metrics (default:False)clamp_db (
Optional[float]) – If provided, the resulting metrics are clamped to be in the range[-clamp_db, clamp_db]load_diag (
Optional[float]) – If provided, this small value is added to the diagonal coefficients of the system metrics when solving for the filter coefficients. This can help stabilize the metric in the case where some of the reference signals may sometimes be zeroreturn_perm (
Optional[bool]) – If set to True, the optimal permutation of the estimated signals is also returned (default:False)change_sign (
Optional[bool]) – If set to True, the sign is flipped and the negative SDR is returned (default:False)
- Return type
Union[ndarray,Tensor]- Returns
sdr – The SDR of the input signal
shape == (..., n_channels_est)perm – The index of the corresponding reference signal
shape == (..., n_channels_est). Only returned ifreturn_perm == True
- fast_bss_eval.sdr_pit_loss(est, ref, filter_length=512, use_cg_iter=None, zero_mean=False, clamp_db=None, load_diag=None)#
Computes the negative signal-to-distortion ratio (SDR) with the PIT loss (permutation invariant training). This means the permutation of sources minimizing the loss is chosen.
This function is similar to
fast_bss_eval.sdr()andfast_bss_eval.sdr_loss(), but with,negative sign to make it a loss function
est/refarguments follow the convention of pytorch loss functions (i.e.,estfirst).pairwise and permutation solving is used (a.k.a. PIT, permutation invariant training)
- Parameters
est (
Union[ndarray,Tensor]) – The estimated signalsshape == (..., n_channels_est, n_samples)ref (
Union[ndarray,Tensor]) – The groundtruth reference signalsshape == (..., n_channels_ref, n_samples)filter_length (
Optional[int]) – The length of the distortion filter allowed (default:512)use_cg_iter (
Optional[int]) – If provided, an iterative method is used to solve for the distortion filter coefficients instead of direct Gaussian elimination. This can speed up the computation of the metrics in case the filters are long. Using a value of 10 here has been shown to provide good accuracy in most cases and is sufficient when using this loss to train neural separation networks.zero_mean (
Optional[bool]) – When set to True, the mean of all signals is subtracted prior to computation of the metrics (default:False)clamp_db (
Optional[float]) – If provided, the resulting metrics are clamped to be in the range[-clamp_db, clamp_db]load_diag (
Optional[float]) – If provided, this small value is added to the diagonal coefficients of the system metrics when solving for the filter coefficients. This can help stabilize the metric in the case where some of the reference signals may sometimes be zero
- Return type
Union[ndarray,Tensor]- Returns
The negative SDR of the input signal after solving for the optimal permutation. This is equivalent to using
sdr_losswithpairwise=Truewith a PIT loss. The returned tensor hasshape == (..., n_channels_est)ifpairwise == False
- fast_bss_eval.sdr_loss(est, ref, filter_length=512, use_cg_iter=None, zero_mean=False, clamp_db=None, load_diag=None, pairwise=False)#
Computes the negative signal-to-distortion ratio (SDR).
This function is almost the same as
fast_bss_eval.sdr()except fornegative sign to make it a loss function
est/refarguments follow the convention of pytorch loss functions (i.e.,estfirst).
- Parameters
est (
Union[ndarray,Tensor]) – The estimated signalsshape == (..., n_channels_est, n_samples)ref (
Union[ndarray,Tensor]) – The groundtruth reference signalsshape == (..., n_channels_ref, n_samples)filter_length (
Optional[int]) – The length of the distortion filter allowed (default:512)use_cg_iter (
Optional[int]) – If provided, an iterative method is used to solve for the distortion filter coefficients instead of direct Gaussian elimination. This can speed up the computation of the metrics in case the filters are long. Using a value of 10 here has been shown to provide good accuracy in most cases and is sufficient when using this loss to train neural separation networks.zero_mean (
Optional[bool]) – When set to True, the mean of all signals is subtracted prior to computation of the metrics (default:False)clamp_db (
Optional[float]) – If provided, the resulting metrics are clamped to be in the range[-clamp_db, clamp_db]load_diag (
Optional[float]) – If provided, this small value is added to the diagonal coefficients of the system metrics when solving for the filter coefficients. This can help stabilize the metric in the case where some of the reference signals may sometimes be zeropairwise (
Optional[bool]) – If set to True, the metrics are computed for every est/ref signals pair (default:False). When set to False, it is expected thatn_channels_ref == n_channels_est.
- Return type
Union[ndarray,Tensor]- Returns
The negative SDR of the input signal. The returned tensor has
shape == (..., n_channels_est)ifpairwise == Falseshape == (..., n_channels_ref, n_channels_est)ifpairwise == True.
- fast_bss_eval.si_bss_eval_sources(ref, est, zero_mean=False, clamp_db=None, compute_permutation=True, load_diag=None)#
This function computes the scale-invariant metrics, SI-SDR, SI-SIR, and SI-SAR, for the input reference and estimated signals.
The order of
ref/estfollows the convention of bss_eval (i.e., ref first).- Parameters
ref (
Union[ndarray,Tensor]) – The estimated signals,shape == (..., n_channels_est, n_samples)est (
Union[ndarray,Tensor]) – The groundtruth reference signals,shape == (..., n_channels_ref, n_samples)zero_mean (
Optional[bool]) – When set to True, the mean of all signals is subtracted prior to computation of the metrics (default:False)clamp_db (
Optional[float]) – If provided, the resulting metrics are clamped to be in the range[-clamp_db, clamp_db]compute_permutation (
Optional[bool]) – When this flag is true, the optimal permutation of the estimated signals to maximize the SIR is computed (default:True)load_diag (
Optional[float]) – If provided, this small value is added to the diagonal coefficients of the system metrics when solving for the filter coefficients. This can help stabilize the metric in the case where some of the reference signals may sometimes be zero
- Return type
Union[Tuple[ndarray,...],Tuple[Tensor,...]]- Returns
si-sdr – The signal-to-distortion-ratio (SDR),
shape == (..., n_channels_est)si-sir – The signal-to-interference-ratio (SIR),
shape == (..., n_channels_est)si-sar – The signal-to-interference-ratio (SIR),
shape == (..., n_channels_est)perm – The index of the corresponding reference signal (only when
compute_permutation == True),shape == (..., n_channels_est)
- fast_bss_eval.si_sdr(ref, est, zero_mean=False, clamp_db=None, return_perm=False, change_sign=False)#
Compute the scale-invariant signal-to-distortion ratio (SI-SDR) only.
This function computes the SDR for all pairs of est/ref signals and finds the permutation maximizing the sum of all SDRs. This is unlike
fast_bss_eval.bss_eval_sources()that uses the SIR.The order of
ref/estfollows the convention of bss_eval (i.e., ref first).- Parameters
ref (
Union[ndarray,Tensor]) – The estimated signals,shape == (..., n_channels_est, n_samples)est (
Union[ndarray,Tensor]) – The groundtruth reference signals,shape == (..., n_channels_ref, n_samples)filter_length – The length of the distortion filter allowed (default:
512)use_cg_iter – If provided, an iterative method is used to solve for the distortion filter coefficients instead of direct Gaussian elimination. This can speed up the computation of the metrics in case the filters are long. Using a value of 10 here has been shown to provide good accuracy in most cases and is sufficient when using this loss to train neural separation networks.
zero_mean (
Optional[bool]) – When set to True, the mean of all signals is subtracted prior to computation of the metrics (default:False)clamp_db (
Optional[float]) – If provided, the resulting metrics are clamped to be in the range[-clamp_db, clamp_db]return_perm (
Optional[bool]) – If set to True, the optimal permutation of the estimated signals is also returned (default:False)change_sign (
Optional[bool]) – If set to True, the sign is flipped and the negative SDR is returned (default:False)
- Return type
Union[ndarray,Tensor]- Returns
si-sdr – The SDR of the input signal
shape == (..., n_channels_est)perm – The index of the corresponding reference signal
shape == (..., n_channels_est). Only returned ifreturn_perm == True
- fast_bss_eval.si_sdr_pit_loss(est, ref, zero_mean=False, clamp_db=None)#
Computes the negative scale-invariant signal-to-distortion ratio (SDR) with the PIT loss (permutation invariant training). This means the permutation of sources minimizing the loss is chosen.
This function is similar to
fast_bss_eval.sdr()andfast_bss_eval.sdr_loss(), but with,negative sign to make it a loss function
est/refarguments follow the convention of pytorch loss functions (i.e.,estfirst).pairwise and permutation solving is used (a.k.a. PIT, permutation invariant training)
- Parameters
est (
Union[ndarray,Tensor]) – The estimated signalsshape == (..., n_channels_est, n_samples)ref (
Union[ndarray,Tensor]) – The groundtruth reference signalsshape == (..., n_channels_ref, n_samples)zero_mean (
Optional[bool]) – When set to True, the mean of all signals is subtracted prior to computation of the metrics (default:False)clamp_db (
Optional[float]) – If provided, the resulting metrics are clamped to be in the range[-clamp_db, clamp_db]
- Return type
Union[ndarray,Tensor]- Returns
The negative SDR of the input signal after solving for the optimal permutation. This is equivalent to using
sdr_losswithpairwise=Truewith a PIT loss. The returned tensor hasshape == (..., n_channels_est)ifpairwise == False
- fast_bss_eval.si_sdr_loss(est, ref, zero_mean=False, clamp_db=None, pairwise=False)#
Computes the negative scale-invariant signal-to-distortion ratio (SI-SDR).
This function is almost the same as
fast_bss_eval.sdr()except fornegative sign to make it a loss function
est/refarguments follow the convention of pytorch loss functions (i.e.,estfirst).
- Parameters
est (
Union[ndarray,Tensor]) – The estimated signalsshape == (..., n_channels_est, n_samples)ref (
Union[ndarray,Tensor]) – The groundtruth reference signalsshape == (..., n_channels_ref, n_samples)zero_mean (
Optional[bool]) – When set to True, the mean of all signals is subtracted prior to computation of the metrics (default:False)clamp_db (
Optional[float]) – If provided, the resulting metrics are clamped to be in the range[-clamp_db, clamp_db]pairwise (
Optional[bool]) – If set to True, the metrics are computed for every est/ref signals pair (default:False). When set to False, it is expected thatn_channels_ref == n_channels_est.
- Return type
Union[ndarray,Tensor]- Returns
The negative SI-SDR of the input signal. The returned tensor has
shape == (..., n_channels_est)ifpairwise == Falseshape == (..., n_channels_ref, n_channels_est)ifpairwise == True.